An Integral Equation Method for the Cahn-Hilliard Equation in the Wetting Problem
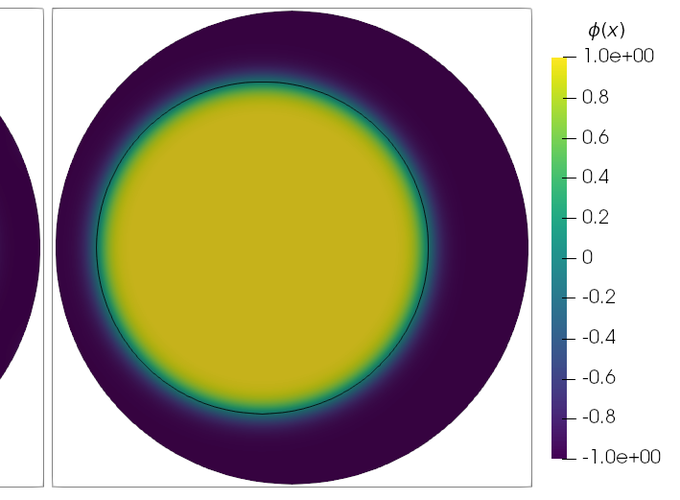 Sample dynamics.
Sample dynamics.
An Integral Equation Method for the Cahn-Hilliard Equation in the Wetting Problem
Abstract
We present an integral equation approach to solving the Cahn-Hilliard equation equipped with boundary conditions that model solid surfaces with certain Young’s angles. Discretization of the system in time using convex splitting leads to a modified biharmonic equation at each time step. To solve it, the basic idea is to split the solution into a volume potential computed with free space kernels, plus the solution to a second kind integral equation (SKIE). The volume potential is evaluated with a box-based volume-FMM method. For non-box domains, source density is extended by solving a biharmonic Dirichlet problem. The near-singular boundary integrals are computed using quadrature by expansion (QBX) with FMM acceleration. Our method has linear complexity and can achieve high order convergence with adaptive refinement. We showcase applications in simulating wetting transition and boundary effects on spinodal decomposition.